Generating simple C++ functions with Genetic Programming
First Blood: Using artificial intelligence to write source code
Available Source code:
- Github Link: Genetic Library
- GitHub Link: SimpleGP (Note that this solution is incomplete and will need some "hacking" to get to work)
As a computer scientist, I spend a lot of time researching source code solutions to problems. Much of this research is something that I do on my own time because ideas need to be proven to be good before you have any chance at getting an investor to come and help you out with extra resources. And, as anybody that has dabbled in coding knows, for every cool “interesting” part of the system you are working on, there are a hundred boring infrastructure elements to develop that are necessary for the thing to work. These boring bits can take a long time and are not particularly fun to develop (things are also a little more exaggerated for me since I am mainly a C++ developer - which I justify by the fact that many of the technologies that I work with need “realtime” performance and using C++ helps). Ultimately, in an ideal world, it would be great to just focus on the critical interesting parts of the program and have all the other boring bits just fall into place without having to worry about them.
The first thing that I did to try and achieve this ideal, is to build a template management tool, which I called SolutionGen. SolutionGen allows me to create boilerplate templates of various solution types (database app, GUI app, console app etc), which would then allow me to start a new project with a bunch of structures already in place. This has saved me some time, but I still found that I was spending a lot of programming time on so-called boring bits.
The next thing that have I started to do is put all the functions that I commonly use into a single library that I called NVLib. This library is available on GitHub here. This library is automatically included in my projects by the templates provided by SolutionGen and it saves me a bunch more time.
But I am still not quite satisfied. One of the things that I have been interested in for a while now, is the notion of using artificial intelligence to generate source code. I think that this could be an interesting area of research, and therefore I am starting to delve deeper into the current ideas around how to achieve this.
An artificial intelligence coder
The work that I present in this article is a very primitive first foray into this problem space. Essentially one of the more well-known approaches to generating source code using artificial intelligence is called genetic programming. Essentially it is a strategy that is inspired by nature and the natural selection of the fittest individuals in a population, leading to overall better genes (for some criteria) within the population. Essentially genetic programming is quite well covered by Wikipedia here.
A problem definition
Before diving into the design choices that I made to set up my genetic programming application, let me describe the test program that I set up to verify the correct operation of my algorithm. The test program was created to verify that my algorithm was able to converge, and was a real-world problem that I have recently coded a solution to.
_Given four corner coordinates of a four-sided polygon (Quadrilateral) in 2D space, in random order, determine which coordinate is the top-left corner. The template function definition is as follows:
int GetTopLeft( double x1, double y1,
double x2, double y2,
double x3, double y3,
double x4, double y4)
The value returned from the function is in the set $i = [1, 2, 3, 4]^{\top}$, where $i$ represents the index of the coordinate that is considered to be the top-left corner. To evaluate how well a particular generated solution performed, I generated a set of test cases in ARFF format (see link here). This allowed me to test the problem on WEKA, to try and determine how difficult it was. A sample of the test file was as follows:
@RELATION tlp
@ATTRIBUTE x1 NUMERIC
@ATTRIBUTE y1 NUMERIC
@ATTRIBUTE x2 NUMERIC
@ATTRIBUTE y2 NUMERIC
@ATTRIBUTE x3 NUMERIC
@ATTRIBUTE y3 NUMERIC
@ATTRIBUTE x4 NUMERIC
@ATTRIBUTE y4 NUMERIC
@ATTRIBUTE class {1, 2, 3, 4}
@DATA
1156,855,685,855,685,298,1156,298,3
663,1007,663,777,942,1007,942,777,2
342,636,1139,636,1139,832,342,832,1
1575,749,1575,1242,840,749,840,1242,3
13,907,13,1615,908,907,908,1615,1
991,194,1560,194,991,858,1560,858,1
1264,793,936,793,936,505,1264,505,3
25,1127,25,900,499,900,499,1127,2
1347,455,994,824,1347,824,994,455,4
The actual file used for training had 500 data test points. Running these test cases against WEKA produced the following results:
| No | Algorithm | Correct |
|---|---|---|
| 1 | ZeroR (Rules) | 28.2% |
| 2 | Conjunctive Rules | 38.8% |
| 3 | JRip (rules) | 69.8% |
| 4 | J48 Tree | 75.4% |
| 5 | J48graft Tree | 75.6% |
| 6 | Functional Tree | 97.6% |
| 7 | Logistic Model Tree | 98.6% |
I chose to formulate the solution as a C++ method that consisted of branch statements (if-else) that either led to a “return” statement or another branch statement at the next level. The condition that the branch statement was evaluated consisted of the structure
<param> <operator> <param> <conjunction> ...
Here param is one of the input parameters (“x1”, “x2”, “x3”, “x4”, “y1”, “y2”, “y3”, “y4”), operator is a logical operator (”==”, “>”, “<”), and conjunction links one expression to another using a conjunction (“||”, “&&”). Both the branch statement and the depth of the program were limited to a depth of five. The following is a “hand-crafted” solution to the problem using the imposed restrictions.
int GetTopLeft( double x1, double y1,
double x2, double y2,
double x3, double y3,
double x4, double y4)
{
if (y1 < y2)
{
if (y1 < y3 && y3 < y4 || y1 == y3)
{
if (x1 < x3) return 1;
else return 3;
}
else
{
if (y1 < y4 && y4 < y3 || y1 == y4)
{
if (x1 < x4) return 1;
else return 4;
}
else
{
if (x3 < x4) return 3;
else return 4;
}
}
}
else
{
if (y1 == y2)
{
if (y1 < y3 && y1 < y4)
{
if (x1 < x2) return 1;
else return 2;
}
else
{
if (y1 < y4)
{
if (x1 < x2) return 1;
else return 2;
}
else
{
if (x3 < x4) return 3;
else return 4;
}
}
}
else
{
if (y2 < y3 && y3 < y4 || y2 == y3 )
{
if (x2 < x3) return 2;
else return 3;
}
else
{
if (y2 < y4 && y4 < y3 || y2 == y4)
{
if (x2 < x4) return 2;
else return 4;
}
else
{
if (x3 < x4) return 3;
else return 4;
}
}
}
}
}
The above code was generated by considering the various cases in which different rules apply to finding the top left point. Some of the cases are shown below in the figure.
 Figure 1: Various Quadrilateral cases that the solution needs to generate.
Figure 1: Various Quadrilateral cases that the solution needs to generate.
The SimpleGP solution
Given the problem described in the previous section, the next step was to try and find an artificial intelligence approach to generating a solution. As stated before, as an initial “benchmark”, it was decided to test using a well-known approach, that while old, was generally recognized as a solution to the problem. That solution is Genetic Programming (as stated above). I have called my algorithm SimpleGP (simple genetic programming). The algorithm generates a tree structure solution based on decision statements (as described in the previous section).
The algorithm was set up to initially generate a random population of 40000 random solutions. Each of these algorithms was tested against the input ARFF file and a score was generated for each potential solution based on the percentage of test cases it solved correctly - therefore a score of 100 was a perfect score. After the first iteration, a next-generation was created by selecting two parents (using a tournament selection see here using a sample size $k=15$). I also decided to try and keep the strongest “genes” within the system by using the notion of elitism (see here).
I also added the notion of mutation into the system. For mutation, I decided to target only the statements that drove the branch functions, simply because this was easy to implement. The way mutation worked was that with a 0.4 probability a solution had a chance that one of its branch statements was selected and either an operator or conjunction was changed to another option.
Results
The goal of this test was simply to see if the algorithm could converge onto a solution with $100%$ accuracy. This was achieved after 24 generations (after the first run once the system had been debugged - which included tracking down a memory leak).
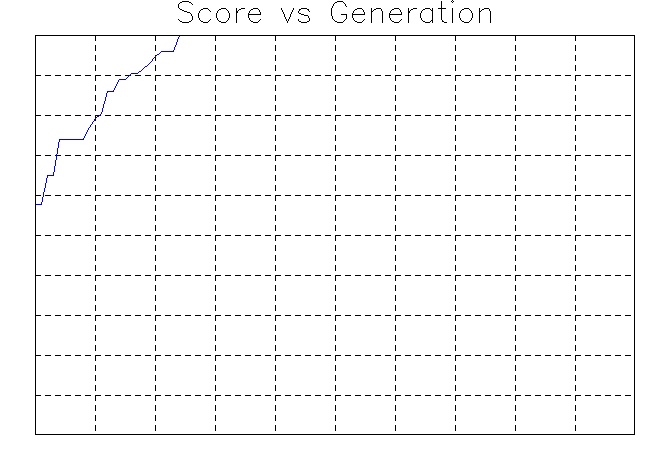 Figure 2: A graph of the convergence rate of the algorithm.
Figure 2: A graph of the convergence rate of the algorithm.
The solution that was generated is the following C++ code:
int GetLeft( double x1, double y1,
double x2, double y2,
double x3, double y3,
double x4, double y4)
{
if (x4 > x1 && x3 < x4 || x2 < x4 || y4 > y3)
{
if (x1 == y1 && x2 < x3 || y3 > y1 || x1 < x3)
{
if (x3 < x2 && x4 == x3 || y2 > y1 && y1 == x3)
{
return 1;
}
else
{
return 2;
}
}
else
{
if (y3 > x4 || x1 == y2 && y4 < y3)
{
if (x1 > x2 && y4 > x1 || x1 > y2 && x4 > x3 && y4 > y3)
{
return 4;
}
else
{
if (x3 < y3 && y4 == x4 && x2 < x1 && y2 > y4)
{
return 3;
}
else
{
return 2;
}
}
}
else
{
if (x4 == y2)
{
return 3;
}
else
{
if (x3 < x1 && y4 < y3 || y4 == y3 || x2 > x1)
{
return 3;
}
else
{
return 4;
}
}
}
}
}
else
{
if (x4 < x1 || y1 > y4 && y3 == x4)
{
if (x4 > x3 && y4 < x2 || y4 > y1)
{
return 2;
}
else
{
if (x3 == y2 && y4 > x3 && y3 < y4)
{
return 2;
}
else
{
return 4;
}
}
}
else
{
return 1;
}
}
}
As is expected, the computer-generated code differs quite a bit from the version created by a human.
Conclusions
The main goal of this work was to try and use an artificial intelligence solution to generate a C++ function to solve a simple “real-world” problem. We set out to do that based on a generated file of “unit-tests”, using the well-known genetic programming algorithm.
The test was successful, our genetic algorithm (called SimpleGP) managed to generate a solution with $100%$ accuracy within 24 generations. The solution that was generated differs quite substantially from the hand-crafted version that I created and had this point I have not done any analysis into the solution to see if there are any new insights to be gained - however, doing that certainly seems like something that should be feasible to do.
The next steps
The main goal of this approach was to perform a basic feasibility test creating computer-generated source code to solve a given problem. In that regard, the experiment was a success. However, this is just the first step in what is expected to be a very long journey. Some of the things lined up next include the following:
- CodeDash is a tool that I am working on for monitoring multiple machine-learning processes online. This tool should be finalized and in place shortly.
- There has been a fair amount of work in the Reinforcement Learning (see here) space on source code generation (which is a more modern approach than the genetic algorithm that I used here), and so I want to explore these approaches as well.
- I am busy establishing this research field and I am documenting the research here (note that this link might be volatile because it links to my lab computer).