Learning how to XOR
Using machine learning to learn XOR

As mentioned in a previous post here, I am interested in using machine learning to speed up software development. The primary approach that I have been looking at in this respect is using machine learning to “learn” functions. The goal is to generate solutions that can be embedded into a source code file and compiled. I am currently more interested in using a data-driven approach (learning from a sample of inputs and their actual outputs) than using a semantic linkage approach like ChatGPT. The main reason is that the data-driven approach fits better with many of the problems that I am trying to solve at the moment. I also like the relationship between this type of learning and test-driven development, which has a proven track record of improving the quality of source code.
Since I have been looking for a solution to embed into source code, I initially thought I needed a machine learning approach representing solutions as source code. This led to the notion of Genetic Programming (GP), of which SimpleGP is an example. However, SimpleGP formulated solutions as tree (using “if” statements), which is limited in its capacity to represent solutions to complex problems. I, therefore, decided to move to a more traditional type of Genetic Programming, which means solutions as mathematical equations (typically encoded as expression trees). While expression trees are still a form of tree learning, the variety of operators for each node is far more varied than basic “if-else” structures, significantly expanding the representation power of these models. My current expression tree-based learning algorithm is VanillaGP.
However, the main argument against GP approaches is that they are slow meandering searches compared to the much faster directed gradient-based approach used by Artificial Neural Networks (ANN). Of course, the cost of utilizing an ANN is that a weighted network is not a particularly familiar or intuitive representation of a solution to a human. There is also the fact that one could argue that the output of a GP algorithm is not particularly user-friendly either - while its solutions do use familiar human symbolic representations (like mathematical equations or source code), these structures are often not formulated in a “human” way, making them hard to understand as well. To understand these trade-offs better, I decided to put together my own ANN (called TrevNet), which is currently under development, but the main library is available here.
The XOR Function
This leads to the notion of the XOR (exclusive OR) function. After assembling the basic components of TrevNet, I wanted to verify that TrevNet was capable of “learning”. To do this, I selected the XOR function as my first test case because:
- It is a simple function, making debugging and analysis easy if things go wrong.
- It is not a linear function, meaning that it is not an entirely straightforward function to learn either.
- It has a history with ANN algorithms - as researchers lost interest in Neural Networks in the 1970s due to the belief that the simple XOR problem could not be resolved by a two-layer ANN (see here).
So what is the XOR function?
XOR is an operation commonly used in boolean algebra. Booleans are normal numbers that are expressed in a number system that represents digits as powers of two (sometimes called base 2), instead of the number system that we are familiar with that represents numbers as columns of powers of ten. Thus a boolean system only has two types of digits, namely zero and one. A number is represented as a sequence of zeros and ones. An example would be that the boolean number 101 = $1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 5$. Boolean algebra is a very convenient system in the field of computing because it maps well to HIGH and LOW voltages in an electric circuit. More famous than XOR, is the OR operation that maps as follows:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Table 1: The truth table for the OR function
While this truth table makes sense to programmers, it does not map well to English. If we say that the options are either A OR B, we typically mean that either A can be true, or B can be true, but not both. XOR modifies the OR truth table to capture this spirit as follows:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Table 2: The truth table for the OR function
In terms of the claim that this function is not linear, one of the tests of linearity is that
\[f(A) + f(B) = f(A + B)\]where clearly
\[f([0,1]^{\top}) + f([1,0]^{\top}) \neq f([1,1])\]VanillaGP
Out of interest, I first wanted to see if VanillaGP was capable of finding an equation that could describe XOR. Turns out that this was a very easy problem for VanillaGP, and it found a solution within its first generation:
\[2 I_1 (I_1 - I_0) + (I_0 - I_1)\]where $I_0$ is the first input and $I_1$ is the second input. This is easy to verify:
- If $I_0 = 0$ and $I_1 = 0$ then clearly the expression is 0.
- If $I_0 = 1$ and $I_1 = 0$ then $2 \times 1 - 1 = 1$.
- If $I_0 = 0$ and $I_1 = 1$ then $0 + 1 = 1$.
- If $I_0 = 1$ and $I_1 = 1$ then $(2 - 2) + (1 - 1) = 0$.
It is interesting to note, that the first time I ran this, the algorithm produced
pow(-p[1], (1 / p[0])) + p[0];
This expression exploits the fact that my C++ version has $pow(-1, \infty) = 1$ (technically I believe the correct answer is undefined because there is no indication whether infinity is even or odd).
I also tried to plot this function. While the true XOR is a boolean function, the formulation here allows a range of numbers to be represented, thus plotting this number in 3D space looks as follows:
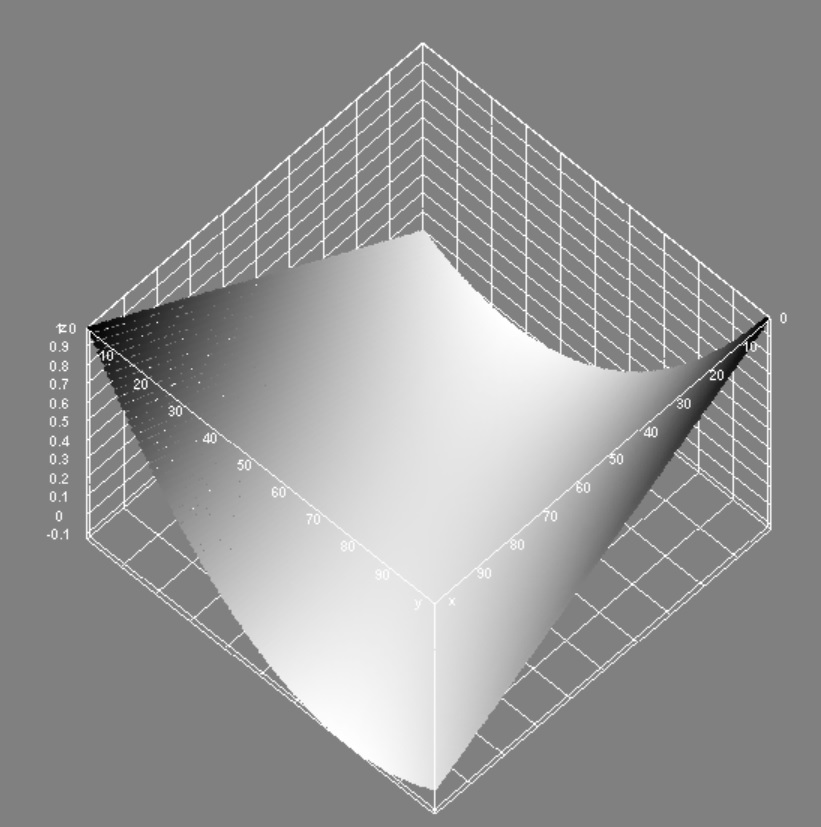
Figure 1: The XOR function is not linear (a linear function would be a plane)
Neural Network
So getting back to TrevNet, the main idea was to use the XOR function to determine whether TrevNet was actually capable of “learning”. The first question that I had, was how big the network needed to be to encode XOR. Armed with the formulation from VanillaGP, I decided to “translate” this expression into a network. Given the equation from VanillaGP, I designed the following network:
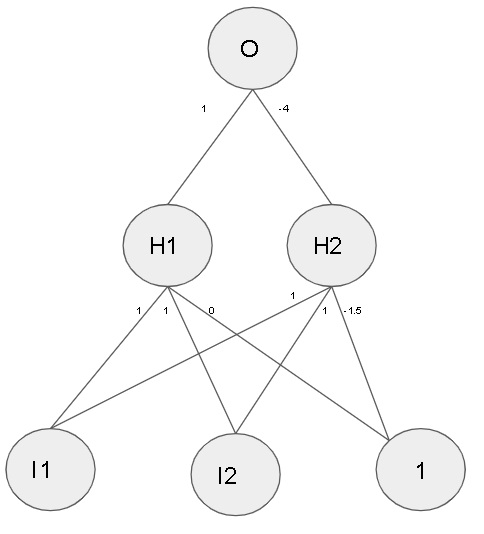
Figure 2: A handcrafted XOR network (with ReLU activation), with I1 and I2 representing the inputs and O as the output
This network can be evaluated as follows (note that ReLU converts negative values to 0):
| I1 | I2 | H1 | H2 | O |
|---|---|---|---|---|
| 0 | 0 | 0 | -1.5 $\rightarrow$ 0 | 0 |
| 0 | 1 | 1 | -0.5 $\rightarrow$ 0 | 1 |
| 1 | 0 | 1 | -0.5 $\rightarrow$ 0 | 1 |
| 1 | 1 | 2 | 0.5 | 0 |
Table 3: Neural network evaluations
Unfortunately, in practice, I was not able to get a 6-node neural network to learn XOR. I suspect that the gradient descent fails due to local minima. This is still something that I want to to investigate. However, I was able to get the network to converge with a 9-node network (hidden layer of 6 and no extra offset input node), in which convergence was achieved within 400 epochs.
I also trained the network on the IRIS dataset, which was able to converge to 95% accuracy after 1000 epochs. This demonstrated that TrevNet was capable of learning. I next added an “embedded” encoding so that TrevNet models can be embedded into strings to be evaluated by source code. The format that I prescribed is a comma-delimited list of edges, where each is a triple (delimited by colons) as
TEST(Network_Test, load_test)
{
// Initialize
auto initString = "0:0:1,0:1:1,1:0:1,1:1:1,2:0:0,2:1:-1.5|0:0:1,1:0:-4|1";
auto network = Network(initString);
// Confirm
ASSERT_FALSE(Eval(network, false, false));
ASSERT_TRUE(Eval(network, false, true));
ASSERT_TRUE(Eval(network, true, false));
ASSERT_FALSE(Eval(network, true, true));
}
/**
* @brief A helper for evaluating the NN
* @param network The actual network
* @param value1 The value that we are dealing with
* @param value2 The value that we are dealing with
* @return true The result that we are dealing with
*/
bool Eval(Network& network, bool value1, bool value2)
{
auto inputs = vector<double> { value1 ? 1.0 : 0.0, value2 ? 1.0 : 0.0, 1.0};
auto output = vector<double>();
network.Evaluate(inputs, output);
return output[0] > 0.5;
}
Looking Forward
So now that I have both VanillaGP and TrevNet in place, the next step is to try try and incorporate machine learning into my development process. Watch this space to see how I do!